GRAND ORAL – Les 3 erreurs à éviter absolument dans votre question

Le Grand Oral : Méthode innovante de préparation – Tome 2

Collection “Le Grand Oral : Méthode innovante de préparation”
Comment visualiser une structure de donnée de type arbre ?
Qu’est-ce qu’un arbre en strucutre de donnée ?
Un arbre est une structure de données hiérarchique qui utilise des noeuds pour stocker des données. Chaque noeud peut avoir un ou plusieurs enfants, mais un seul parent. Le noeud sans parent est appelé la racine de l’arbre. Les noeuds qui n’ont pas d’enfant sont appelés feuilles. Les arbres peuvent être utilisés pour stocker des données de manière organisée et efficace, comme dans les arbres de recherche binaire ou les arbres de décision.
A quoi servent les arbres en en strucutre de donnée ?
Les arbres en structure de données sont utilisés pour stocker et organiser des données de manière hiérarchique. Cela permet de faciliter les opérations de recherche, de tri et de modification des données. Il existe plusieurs types d’arbres, chacun ayant des utilisations spécifiques :
-
Les arbres de recherche binaire (BST) sont utilisés pour stocker des données numériques ou de chaîne de caractères de manière ordonnée. Cela permet de rapidement rechercher des données spécifiques en utilisant une technique de parcours de l’arbre appelée “recherche binaire”.
-
Les arbres de décision sont utilisés pour représenter des systèmes de prise de décision basés sur des conditions. Ils sont souvent utilisés dans les systèmes d’IA pour prendre des décisions en fonction de données entrantes.
-
Les arbres de recherche triés (Trie) sont utilisés pour stocker des mots ou des chaînes de caractères de manière ordonnée. Ce qui permet de faire des recherches rapides de mots ou des préfixes de mots.
-
Les arbres de Huffman sont utilisés pour compresser des données en utilisant des codes binaires pour représenter les caractères les plus fréquents avec moins de bits.
Il existe d’autres types d’arbres tels que les arbres AVL, les arbres rouge-noir, les arbres de suffixes, etc. Chacun d’eux a des utilisations spécifiques dans différents domaines.
Comment visualiser un arbre en structure de donnée ?
Il existe plusieurs façons de visualiser un arbre en structure de données. La plus courante est de représenter chaque noeud sous forme de cercle ou de rectangle, et de relier les noeuds parents aux noeuds enfants avec des lignes. La racine de l’arbre est généralement en haut, et les feuilles sont en bas.

Dans cet exemple, le noeud 5 est la racine de l’arbre, les noeuds 3 et 8 sont les enfants de la racine, et les noeuds 2 et 4 sont les enfants du noeud 3.
Il existe également des logiciels qui permettent de visualiser les arbres en 3D ou en utilisant des animations pour montrer comment les données sont insérées et supprimées dans l’arbre.
Il existe aussi des outils pour visualiser des arbres de décision ou des arbres de recherche triée. Pour ces types d’arbre, les noeuds sont représentés par des conditions ou des caractères, et les branches représentent les différentes valeurs possibles pour ces conditions ou caractères.
Comment visualiser un arbre en Python ?
Dans cet article, je vous présente un outil simple de visualisation de structures de données en Python le module lolviz.
Ce module essaie de rechercher et de formater joliment les structures de données communes comme les arbres. Ce paquet est principalement destiné à être utilisé dans l’enseignement et les présentations avec les carnets Jupyter, mais pourrait également être utilisé pour le débogage des structures de données.
Il semble important de décrire et de visualiser aux étudiants comment les données sont disposées en mémoire. Il existe de très bons outils de visualisation des structures de données, mais celui-ci peut-être utilisé via Python dans les carnets Jupyter.
L’apparence et l’idée ont été inspirées par l’impressionnant Python tutor.
from lolviz import *
class ArbreBinaire:
def __init__(self,racine,filsGauche,filsDroit):
self.racine = racine
self.filsGauche = filsGauche
self.filsDroit = filsDroit
tree = ArbreBinaire ('A',
ArbreBinaire('B',ArbreBinaire('D',None,None),ArbreBinaire('E',ArbreBinaire('G',None,None),ArbreBinaire('H',None,None))),
ArbreBinaire('C',ArbreBinaire('-',None,None),ArbreBinaire('F',ArbreBinaire('I',None,None),ArbreBinaire('-',None,None))))
display(treeviz(tree))Voici le résultat.

Pour aller plus loin
Pour approfondir vos connaissances, et développer vos compétences, je vous propose cette sélection de livre.
Comment ChatGPT peut vous aider à réussir votre épreuve du grand oral ?

Comment créer un argumentaire avec ChatGPT ?
Le grand oral est l’une des épreuves importantes du bac. Pour réussir, il est essentiel de présenter des arguments solides pour justifier votre position sur un sujet donné. Mais comment pouvez-vous être sûr que vos arguments sont convaincants et bien étayés ? C’est là que ChatGPT peut vous aider.
ChatGPT est un modèle de langage de pointe qui peut être utilisé pour extraire les raisons qui justifient une position dans un texte. En utilisant ChatGPT pour analyser un article ou un texte en rapport avec la question qui vous est posée, vous pouvez identifier les arguments clés et les points importants qui vous aideront à construire un discours solide et convaincant.
Pour vous aider à mieux comprendre comment ChatGPT peut vous aider à réussir votre épreuve du grand oral, j’ai créé une vidéo de démonstration. Dans cette vidéo, vous découvrirez comment utiliser ChatGPT pour extraire les raisons qui justifient une position dans un texte et comment utiliser ces informations pour rédiger un discours structuré et convaincant.
Si vous êtes en train de préparer votre épreuve du grand oral, cette vidéo est un outil inestimable pour vous aider à réussir. Visionnez la vidéo dès maintenant et découvrez comment ChatGPT peut vous aider à extraire les raisons qui justifient une position dans un texte pour rédiger un discours convaincant et bien structuré.
Optimisez vos résultats de ChatGPT avec les bons prompts: la clé pour des réponses précises et rapides
Vous voulez obtenir des réponses précises et rapides à vos questions ? Vous souhaitez réduire le temps nécessaire pour entraîner ChatGPT ? Vous voulez adapter votre modèle aux besoins spécifiques de votre de votre projet ? Alors, vous avez besoin d’un bon prompt !
Le bon prompt est la clé pour extraire les raisons qui justifient une position dans un texte. En créant des prompts bien formulés, vous pouvez aider ChatGPT à comprendre clairement ce que vous voulez et à fournir des réponses de haute qualité. En outre, le bon prompt peut vous aider à réduire le temps d’entraînement de votre modèle, à personnaliser votre modèle pour répondre aux besoins spécifiques de votre projet.
Ne laissez pas un prompt mal conçu ruiner votre travail. Investissez dans l’apprentissage de l’écriture d’un bon prompt pour améliorer la qualité de vos réponses, gagner du temps, et adapter ChatGPT aux besoins spécifiques de votre projet.
Prêt à transformer votre préparation au grand oral ? 🚀
Si vous avez trouvé cet article utile, vous allez adorer “Le Grand Oral : Rapide et facile avec ChatGPT“. Ce guide n’est pas seulement un livre, c’est votre passeport pour exceller lors de l’épreuve cruciale du baccalauréat. Grâce à des techniques innovantes et des conseils pratiques issus de la technologie avancée de ChatGPT, ce livre est conçu spécifiquement pour les lycéens désireux de maximiser leur performance.
Ne laissez rien au hasard pour cette épreuve déterminante. Cliquez ici pour obtenir votre exemplaire sur Amazon et commencez à préparer votre présentation avec confiance et aisance. Saisissez l’opportunité de faire de votre grand oral un moment de succès retentissant !
Grand oral: Comment ChatGPT peut vous aider à rédiger le texte de votre discours ?

Dans cet article, je vous présenterai mon argumentaire sur cette problématique et vous expliquerai comment ChatGPT, notre assistant virtuel, peut vous aider à renforcer vos propres arguments pour défendre votre position.
Pour cela, je me suis appuyer sur l’article:
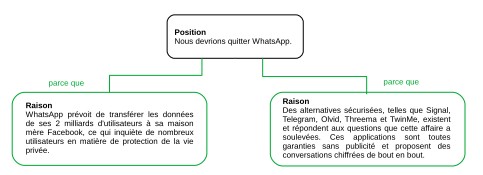
Voici une ébauche à personnaliser pour la première raison principale.
WhatsApp prévoit de transférer les données de ses 2 milliards d’utilisateurs à sa maison mère Facebook, ce qui inquiète de nombreux utilisateurs en matière de protection de la vie privée.
- Texte rédigé par ChatGPT
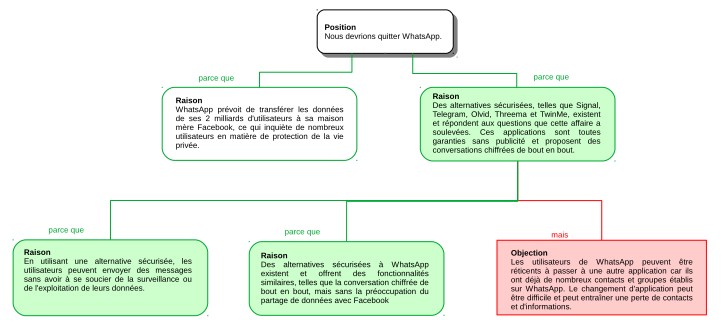
La première raison pour quitter WhatsApp est que l’entreprise prévoit de transférer les données de ses utilisateurs à Facebook. En partageant les données, cela peut potentiellement compromettre la vie privée des utilisateurs de WhatsApp. Il est important de souligner que Facebook a été impliqué dans plusieurs scandales de protection de la vie privée, ce qui peut inquiéter les utilisateurs de WhatsApp. En conséquence, il est légitime pour les utilisateurs de WhatsApp de s’inquiéter de savoir comment leurs données seront utilisées et protégées par Facebook.
La deuxième raison pour quitter WhatsApp est le manque de contrôle des utilisateurs sur les données que l’entreprise partage avec Facebook. Bien que WhatsApp ait promis de protéger la vie privée de ses utilisateurs lors de son acquisition par Facebook en 2014, elle a commencé à partager les données de ses utilisateurs avec d’autres entreprises du groupe en 2016. Les utilisateurs ont peu de contrôle sur les données partagées avec Facebook, ce qui est inquiétant car il est important que les utilisateurs aient le contrôle sur leurs propres données.
Cependant, il est important de noter que WhatsApp a reporté la mise à jour controversée de ses conditions d’utilisation en ce qui concerne le partage de données avec Facebook. Cela pourrait indiquer une volonté de l’entreprise de respecter la vie privée de ses utilisateurs. Cependant, cela ne garantit pas que les utilisateurs de WhatsApp sont protégés à long terme contre l’utilisation de leurs données par Facebook. Il est également important de souligner que WhatsApp a déjà partagé des données avec d’autres entreprises du groupe Facebook en 2016, ce qui montre que les utilisateurs ne peuvent pas avoir confiance en l’entreprise pour protéger leurs données.
En conclusion, pour garantir une protection efficace de la vie privée des utilisateurs, il est recommandé de quitter WhatsApp. Les utilisateurs ont peu de contrôle sur les données partagées avec Facebook, ce qui rend leur vie privée potentiellement vulnérable. Bien que WhatsApp ait reporté la mise à jour controversée de ses conditions d’utilisation, cela ne garantit pas que les utilisateurs sont protégés à long terme contre l’utilisation de leurs données par Facebook. Les utilisateurs doivent être conscients de l’importance de la protection de leur vie privée et être prêts à prendre des mesures pour protéger leurs données en ligne.

Pour aller plus loin
- Comment ChatGPT peut vous aider à réussir votre épreuve du grand oral ?
- Comment utiliser Chat GPT pour l’épreuve du Grand oral ?
- Comment rédiger le texte de son discours pour le Grand oral avec ChatGPT ?
ChatGPT est un outil puissant qui peut vous aider à rédiger un texte à partir d’un argumentaire de manière efficace et fluide. Voici comment vous pouvez utiliser ChatGPT pour cela :
-
Structurez votre argumentaire : Avant de commencer à utiliser ChatGPT, organisez votre argumentaire en points clés et en sous-arguments. Cela vous aidera à fournir des instructions claires à ChatGPT.
-
Commencez l’interaction avec ChatGPT : Vous pouvez démarrer la conversation en fournissant un contexte clair à ChatGPT, par exemple : “J’ai besoin d’aide pour rédiger un texte sur le sujet suivant : [thème du sujet]. Voici mon argumentaire : [présentez brièvement votre argumentaire].”
-
Posez des questions spécifiques : Utilisez des questions spécifiques pour obtenir des informations ou des exemples supplémentaires. Par exemple : “Pouvez-vous me fournir des statistiques sur l’utilisation de WhatsApp ?” ou “Quels sont les avantages et les inconvénients de WhatsApp par rapport à d’autres messageries instantanées ?”
-
Demandez des suggestions pour la structure et les transitions : Si vous avez besoin d’aide pour structurer votre texte ou pour trouver des transitions entre les idées, demandez à ChatGPT des suggestions spécifiques. Par exemple : “Comment puis-je introduire mon premier argument de manière convaincante ?” ou “Quelle serait une bonne transition entre mes deuxième et troisième points ?”
-
Relecture et affinement : Une fois que ChatGPT vous a fourni une réponse, relisez-la attentivement, identifiez les parties pertinentes pour votre texte et apportez les modifications nécessaires pour l’adapter à votre style d’écriture et à votre argumentaire initial.
Il est important de noter que, bien que ChatGPT soit un outil puissant, il peut parfois générer des réponses qui ne sont pas totalement précises ou appropriées. Il est donc essentiel de faire preuve de discernement et de revoir attentivement le contenu généré par ChatGPT afin de l’adapter à vos besoins spécifiques.
En utilisant ChatGPT comme un compagnon de rédaction, vous pouvez bénéficier de ses capacités à générer du texte de manière cohérente et à fournir des informations supplémentaires pour renforcer votre argumentaire. Cependant, n’oubliez pas que la rédaction d’un texte reste une tâche qui nécessite votre créativité et votre expertise. ChatGPT est là pour vous assister et vous inspirer, mais il est important de conserver votre voix et votre style dans votre propre écriture.
Pour aller plus loin
Vous voulez en savoir plus sur le “TD – Faut-il quitter la messagerie instantanée Whatsapp ?” et comment ChatGPT peut vous aider à préparer votre présentation orale pour le baccalauréat ? Ne manquez pas cette opportunité de découvrir comment cette technologie peut faciliter votre travail et améliorer votre performance. Inscrivez-vous dès maintenant pour en savoir plus et recevoir des conseils supplémentaires pour réussir votre épreuve orale et obtenir le texte de ce discours pour le Grand oral. Remplissez simplement le formulaire ci-dessous.
Prêt à transformer votre préparation au grand oral ? 🚀
Si vous avez trouvé cet article utile, vous allez adorer “Le Grand Oral : Rapide et facile avec ChatGPT“. Ce guide n’est pas seulement un livre, c’est votre passeport pour exceller lors de l’épreuve cruciale du baccalauréat. Grâce à des techniques innovantes et des conseils pratiques issus de la technologie avancée de ChatGPT, ce livre est conçu spécifiquement pour les lycéens désireux de maximiser leur performance.
Ne laissez rien au hasard pour cette épreuve déterminante. Cliquez ici pour obtenir votre exemplaire sur Amazon et commencez à préparer votre présentation avec confiance et aisance. Saisissez l’opportunité de faire de votre grand oral un moment de succès retentissant !
Comment préparer le Grand oral avec ChatGPT ?

Êtes-vous prêt à maîtriser l’art de l’éloquence et à briller lors de vos discours ? Imaginez captiver votre auditoire, exprimer vos idées avec assurance et laisser une impression durable. Si vous êtes un élève de terminale se préparant pour l’épreuve du grand oral au baccalauréat, nous avons une ressource exclusive qui vous aidera à atteindre ces objectifs.
Bienvenue dans l’échantillon gratuit de mon e-book ’15 exemples de texte de discours pour le grand oral au baccalauréat’ ! Cet échantillon est conçu spécialement pour vous, pour vous donner un avant-goût de la puissance et de l’impact de nos conseils et exemples concrets.
Imaginez-vous parcourant les pages de cet échantillon, découvrant des discours captivants, des structures persuasives et des idées percutantes. Vous aurez accès à une sélection de nos meilleurs exemples de discours, soigneusement choisis pour vous aider à comprendre les techniques clés et à vous inspirer pour la rédaction de vos propres discours.
Nous croyons fermement que la réussite lors de l’épreuve du grand oral repose sur la préparation et la confiance. C’est pourquoi nous avons créé cet échantillon gratuit afin que vous puissiez vous familiariser avec notre approche unique et sentir l’impact positif qu’elle peut avoir sur votre performance.
N’attendez plus ! Téléchargez dès maintenant votre échantillon gratuit et découvrez par vous-même comment nos exemples de discours peuvent vous aider à briller lors de l’épreuve du grand oral. Que vous soyez à la recherche d’idées percutantes, de structures efficaces ou de conseils pratiques, notre échantillon gratuit est là pour vous guider sur la voie de la réussite.
Préparez-vous à impressionner le jury, à captiver votre auditoire et à faire briller votre éloquence. Téléchargez votre échantillon gratuit dès maintenant et commencez votre voyage vers le succès lors de l’épreuve du grand oral au baccalauréat !
Guide Ultime pour Exceller au Grand Oral du Baccalauréat : Découvrez nos 15 Exemples de Discours et Astuces Pratiques
Ce guide complet a été spécialement conçu pour vous, élèves de terminale, qui aspirez à exceller lors de l’épreuve du grand oral au baccalauréat.
Dans cet e-book, nous avons rassemblé 15 exemples de discours soigneusement sélectionnés, chacun présentant une structure persuasive et des idées puissantes. Ces exemples couvrent une variété de sujets pertinents et actuels, vous offrant une large gamme de possibilités pour votre propre préparation.
Chaque exemple de discours est accompagné d’une analyse détaillée qui met en évidence les techniques clés utilisées pour captiver l’auditoire, structurer les idées et transmettre un message percutant. Vous apprendrez comment créer un impact mémorable grâce à des techniques de rhétorique, d’utilisation efficace de la voix, de gestuelle et bien plus encore.
Ce n’est pas seulement un recueil de discours, c’est un guide complet qui vous aidera à comprendre les mécanismes sous-jacents d’un discours réussi. Vous découvrirez comment construire une introduction captivante, développer des arguments convaincants et conclure de manière percutante. Nos conseils pratiques vous guideront tout au long du processus de préparation et vous donneront les outils nécessaires pour briller lors de votre présentation.
Que vous soyez novice dans l’art de l’éloquence ou que vous cherchiez à perfectionner vos compétences existantes, notre e-book vous fournira les connaissances et les exemples nécessaires pour vous démarquer de la masse et impressionner le jury.
Nous sommes convaincus que cet e-book deviendra votre allié indispensable dans la préparation de l’épreuve du grand oral. Il vous permettra d’acquérir une compréhension approfondie des stratégies gagnantes, d’améliorer votre confiance en vous et de vous démarquer parmi vos pairs.
Préparez-vous à transformer votre façon de présenter et à faire une impression durable lors de l’épreuve du grand oral. Ne manquez pas cette opportunité unique de découvrir les secrets des discours réussis.
Prêt à transformer votre préparation au grand oral ? 🚀
Si vous avez trouvé cet article utile, vous allez adorer “Le Grand Oral : Rapide et facile avec ChatGPT“. Ce guide n’est pas seulement un livre, c’est votre passeport pour exceller lors de l’épreuve cruciale du baccalauréat. Grâce à des techniques innovantes et des conseils pratiques issus de la technologie avancée de ChatGPT, ce livre est conçu spécifiquement pour les lycéens désireux de maximiser leur performance.
Ne laissez rien au hasard pour cette épreuve déterminante. Cliquez ici pour obtenir votre exemplaire sur Amazon et commencez à préparer votre présentation avec confiance et aisance. Saisissez l’opportunité de faire de votre grand oral un moment de succès retentissant !
Comment utiliser Chat GPT pour l’épreuve du Grand oral ?

L’épreuve orale du baccalauréat exige que les étudiants présentent leur travail de recherche ou leur projet devant un jury, qui évalue leur capacité à s’exprimer clairement et à défendre leurs idées. La préparation de cette présentation orale peut être une tâche difficile pour de nombreux étudiants, surtout lorsqu’il s’agit de rédiger le texte de leur discours.
C’est dans ce contexte que l’utilisation de l’intelligence artificielle (IA) pour la rédaction de texte peut offrir une solution efficace. Les systèmes de génération de texte basés sur l’IA, comme ChatGPT, peuvent aider les étudiants à rédiger leur présentation orale en leur proposant du contenu à partir de leurs instructions et de leur contenu de recherche. Cette utilisation de l’IA peut faciliter la tâche de rédaction pour les étudiants et les aider à préparer une présentation orale réussie. Dans cet article, nous examinerons plus en détail comment ChatGPT peut être utilisé pour la rédaction du texte d’une présentation orale pour l’épreuve du baccalauréat.
1. Qu’est-ce que Chat GPT ?
Chat GPT (Generative Pre-trained Transformer) est une technologie d’intelligence artificielle développée par OpenAI, qui permet de générer du texte de manière autonome. Cette technologie utilise un modèle de langage basé sur les réseaux de neurones, qui a été pré-entraîné sur de vastes corpus de texte. En utilisant ces corpus, Chat GPT est capable de prédire la probabilité d’une séquence de mots étant la suite logique d’une phrase donnée.
Le fonctionnement de Chat GPT repose sur l’entrée d’un texte ou d’une phrase, suivi de la prédiction de la suite logique la plus probable de cette phrase. L’algorithme utilise une technique appelée “décodage auto-régressif” pour générer du texte, en prédisant chaque mot un à un en se basant sur les mots précédents de la phrase. Cette technique permet à Chat GPT de générer des textes de manière autonome, avec une qualité et une cohérence proches de celles de l’écriture humaine.
2. Comment utiliser ChatGPT pour rédiger le texte d’une présentation orale
Si vous êtes un élève qui se prépare à passer l’épreuve orale du baccalauréat, ou un enseignant qui souhaite aider ses élèves à préparer leur présentation orale, ChatGPT peut être un outil utile pour la rédaction de texte. Voici les étapes pour utiliser ChatGPT :
- Tout d’abord, accédez à la plateforme ChatGPT et créez un compte si nécessaire.
- Ensuite, sélectionnez l’option “génération de texte” pour accéder à la fonction de génération de texte de ChatGPT.
- Entrez le sujet de votre présentation orale, ainsi que toutes les informations que vous souhaitez inclure dans le texte généré. Vous pouvez également préciser le style de langage que vous souhaitez utiliser (formel ou informel).
- Après avoir entré ces informations, ChatGPT générera automatiquement un texte pour votre présentation orale.
- Vous pouvez personnaliser le texte généré en l’éditant ou en ajoutant des informations supplémentaires. Vous pouvez également demander à ChatGPT de générer un nouveau texte en entrant des instructions plus spécifiques.
Il est important de noter que ChatGPT n’est pas parfait et peut parfois générer du texte qui n’est pas adapté à votre présentation orale. C’est pourquoi il est important de personnaliser le texte généré pour répondre à vos besoins spécifiques.
Enfin, pour utiliser ChatGPT de manière efficace pour la rédaction du texte d’une présentation orale, il est important d’entrer des informations claires et précises. Assurez-vous que les informations que vous fournissez à ChatGPT sont pertinentes pour votre présentation orale et qu’elles sont organisées de manière cohérente. De cette façon, vous pouvez vous assurer que le texte généré par ChatGPT répondra à vos besoins de manière efficace et précise.

3. – TD – Faut-il quitter la messagerie instantanée Whatsapp ?
Les réseaux sociaux font désormais partie intégrante de notre quotidien. Parmi eux, la messagerie instantanée Whatsapp est l’une des plus populaires. Mais récemment, une question se pose : faut-il quitter cette messagerie instantanée ? Cette question est au cœur de notre activité pédagogique destinée aux élèves de la classe de terminale de spécialité NSI.
Objectif :
L’objectif de cette activité est de permettre aux élèves de rédiger le texte d’un discours de 5 minutes expliquant l’une des deux positions : “Il faut quitter la messagerie instantanée Whatsapp” ou “Il ne faut pas quitter la messagerie instantanée Whatsapp”. Les élèves devront utiliser uniquement l’article de presse “Messageries instantanées : et si on quittait WhatsApp ?” comme support pédagogique.
Méthodologie :
Cette activité pédagogique vise à amener une méthodologie de construction étape par étape d’un discours argumenté à partir d’un texte en utilisant Chat GPT. Les élèves devront tout d’abord lire attentivement l’article de presse et identifier les arguments en faveur ou contre le fait de quitter Whatsapp. Ensuite, ils devront utiliser Chat GPT pour générer un texte en suivant les étapes décrites précédemment.
Compétences évaluées :
Cette activité permettra d’évaluer les compétences suivantes :
- La qualité des connaissances des élèves sur le sujet des réseaux sociaux et de la messagerie instantanée Whatsapp en particulier ;
- La qualité et la construction de l’argumentation dans le discours rédigé par les élèves.
Conclusion :
Cette activité pédagogique permettra aux élèves de développer leurs compétences en matière de recherche documentaire, de synthèse et de rédaction d’un discours argumenté. L’utilisation de Chat GPT permettra aux élèves de bénéficier d’un outil puissant pour générer du contenu textuel de qualité. En fin de compte, cette activité permettra aux élèves de se forger leur propre opinion sur la question de savoir s’il faut quitter ou non la messagerie instantanée Whatsapp.
Vous voulez en savoir plus sur le “TD – Faut-il quitter la messagerie instantanée Whatsapp ?” et comment ChatGPT peut vous aider à préparer votre présentation orale pour le baccalauréat ? Ne manquez pas cette opportunité de découvrir comment cette technologie peut faciliter votre travail et améliorer votre performance. Inscrivez-vous dès maintenant pour en savoir plus et recevoir des conseils supplémentaires pour réussir votre épreuve orale. Remplissez simplement le formulaire ci-dessous.
4. Bilan
L’utilisation de ChatGPT pour rédiger le texte d’une présentation orale pour le baccalauréat peut être un outil extrêmement utile pour les étudiants et les enseignants. Les avantages sont nombreux, notamment la possibilité de gagner du temps, de fournir un contenu de qualité et d’offrir un support pour les étudiants ayant des difficultés à rédiger un texte.
Cependant, il est important de rappeler que ChatGPT ne doit pas être utilisé comme une solution facile ou comme une méthode de plagiat. Il est également essentiel de comprendre le contenu que vous présentez afin de pouvoir répondre aux questions et aux commentaires de votre auditoire.
En fin de compte, l’IA a le potentiel d’améliorer considérablement l’éducation, mais il est important de l’utiliser de manière responsable et de manière à compléter les méthodes d’enseignement existantes plutôt que de les remplacer. L’objectif final est de fournir aux élèves les meilleures ressources et les meilleurs outils possibles pour les aider à réussir leur parcours éducatif.
Prêt à transformer votre préparation au grand oral ? 🚀
Si vous avez trouvé cet article utile, vous allez adorer “Le Grand Oral : Rapide et facile avec ChatGPT“. Ce guide n’est pas seulement un livre, c’est votre passeport pour exceller lors de l’épreuve cruciale du baccalauréat. Grâce à des techniques innovantes et des conseils pratiques issus de la technologie avancée de ChatGPT, ce livre est conçu spécifiquement pour les lycéens désireux de maximiser leur performance.
Ne laissez rien au hasard pour cette épreuve déterminante. Cliquez ici pour obtenir votre exemplaire sur Amazon et commencez à préparer votre présentation avec confiance et aisance. Saisissez l’opportunité de faire de votre grand oral un moment de succès retentissant !
Comment devenir un bon professeur de NSI ?