Tableau de Karnaugh
Un tableau de Karnaugh est un outil graphique permettant de simplifier graphiquement des équations logiques. Cette méthode a été développée par Maurice Karnaugh en 1953.
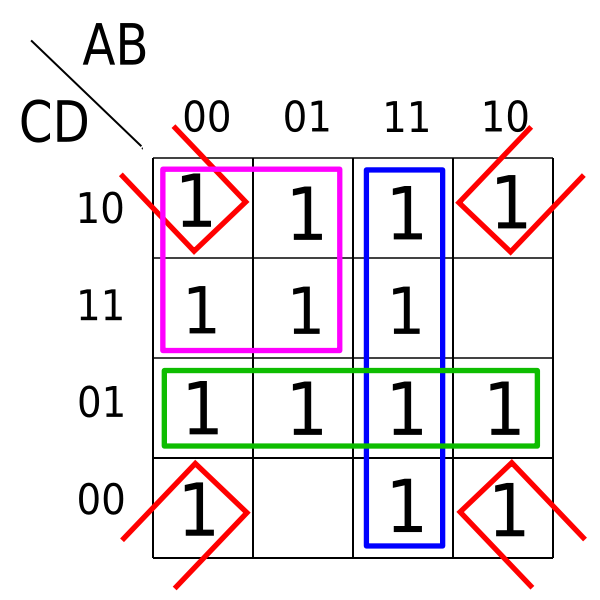
Une table de Karnaugh peut être vu comme une table de vérité particulière, à deux dimensions, destinées à faire apparaître visuellement les simplifications possibles.
Deux méthodes de simplification
Pour déterminer l’expression logique, on peut utiliser 2 méthodes
- former une somme ;
- former un produit.
La méthode former par une somme
Pour trouver l’équation, il faut regrouper les valeurs de S égales à 1. Les groupes formés doivent être les moins nombreux possibles, mais ils doivent englober tous les 1.
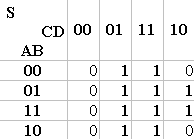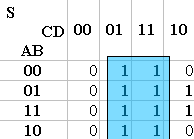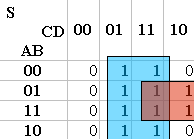
Pour terminer, on fait la somme des groupes formées (somme de produit).
Cette méthode simple et rapide, permet de trouver une équation visuellement, et propose une alternative à la simplification d’équation (calcul booléen) , qui peut rapidement devenir fastidieuse.
La méthode former par un produit
Pour trouver l’équation, il faut regrouper les valeurs de S égales à 0.
En regroupant les 0, on trouve S’ sous forme d’une somme, et par complémentation, on obtient S sous forme de produit (produit de somme).
Application Android ” FLX Karnaugh“
J’ai testé la version gratuite 1.1. Pour l’installer sur votre Smartphone ou sur votre tablette, vous avez besoin de la version Android 3 ou une version ultérieure. Vous pouvez la télécharger en cliquent ici.
 L’application Android ” FLX Karnaugh ” est gratuite et comme toute application de ce genre, vous recevrez de temps en temps de la publicité, mais elle ne gêne en rien son utilisation.
L’application Android ” FLX Karnaugh ” est gratuite et comme toute application de ce genre, vous recevrez de temps en temps de la publicité, mais elle ne gêne en rien son utilisation.
Pour présenter les fonctionnalités de l’application ” FLX Karnaugh ” j’utiliserai l’épreuve de Mathématiques pour l’informatique Session 2013 Métropole du BTS Services Informatiques aux Organisations.
Cette épreuve de 2 heures comportée 3 partie, nous nous concentrons ici sur uniquement la première partie.
BTS SIO – 2013 – Epreuve E21 – Mathématiques pour l’informatique
Cette épreuve de 2 heures comportée 3 partie. Nous nous concentrons ici sur uniquement le premier exercice. Vous pouvez télécharger en cliquant ici.
Exercice 1 (6 points)
Le directeur des ressources humaines (DRH) d’une mairie doit recruter une personne pour un travail concernant la circulation des voitures dans le centre-ville.
Partie A
Pour faire son choix, le DRH met en place trois critères de sélection concernant les connaissances en informatique, l’expérience dans le domaine concerné et le suivi d’un stage de formation spécifique.
La personne recrutée devra:
- avoir des connaissances informatiques et de l’expérience dans le domaine concerné;
- ou ne pas avoir de connaissances informatiques, mais avoir suivi un stage de formation spécifique;
- ou ne pas avoir d’expérience dans le domaine concerné, mais avoir suivi un stage de formation spécifique.
On définit les trois variables booléennes a, b et c suivantes :
- a =1 si la personne possède des connaissances informatiques, a =0 sinon;
- b = 1 si la personne possède de l’expérience dans le domaine concerné, b = 0 sinon;
- c = 1 si la personne a suivi un stage de formation spécifique, c=0 sinon.
- Décrire la situation correspondant au produit a.b./c
a.b./c signifie que la personne possède des connaissances informatiques (a=1) et de l’expérience dans le domaine concerné (b=1), mais n’a pas suivi de stage spécifique de formation (c=0).
- Définir l’expression booléenne E correspondant aux critères de sélection du DRH.
E = a.b + /a.c + b.c
- Sous forme littérale, on obtient :
Le DRH veut que :
la personne possède des connaissances informatiques (a=1) ET de l’expérience dans le domaine concerné (b=1)
OU
la personne ne possède pas des connaissances informatiques (a=0) ET la personne a suivi un stage de formation spécifique (c=1)
OU
la personne a de l’expérience dans le domaine concerné (b=1) ET a suivi un stage de formation spécifique (c=1)
- À l’aide d’un diagramme de Karnaugh ou d’un calcul booléen, trouver une écriture simplifiée de l’expression booléenne E sous la forme d’une somme de deux termes.
- Tableau de Karnaugh (méthode graphique)
Pour cette méthode, nous utiliserons l’application Android “FLX Karnaugh“
L’application est simple d’utilisation; Vous sélectionnez le nombre de variables (inputs), vous compléter votre table de vérité et vous obtenez le tableau de Karnaugh avec les regroupement et en bas de l’écran l’équation simplifier S = a.b + c.
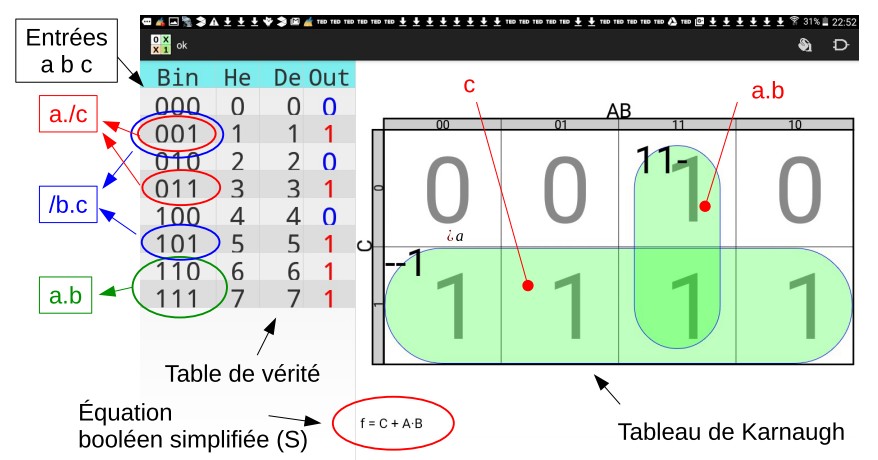
- Calcul booléen (algèbre de Boole)
Je propose d’utiliser un outil que je vous ai déjà présenté dans d’autres billets à savoir Wolfram Alpha à l’adresse suivante: http://www.wolframalpha.com/
Saisissez votre expression booléen dans la barre de saisie de Wolfram alpha.
- or = fonction logique OU
- and = fonction logique ET
- ~ = fonction NON
L’outil en ligne vous renvoie comme résultats:
- La table de vérité (truth table);

Notation: “T” = “True” = “1” et “F”= “False” = “0”
- L’équation simplifiée (DNF);

NB: cliquer sur le bouton “text notation” pour afficher les fonctions logiques.
etc…
Par les deux méthodes, on obtient bien le même résultat: E = a.b + c
- Écrire une phrase donnant les conditions de recrutement correspondant à la simplification précédente de l’expression booléenne E.
La personne possède des connaissances informatiques (a=1) et de l’expérience dans le domaine concerné (b=1) OU a suivi un stage de formation spécifique (c=1).



