Qu’est-ce la méthode récursive en python ?

La méthode récursive en Python est une technique de programmation qui consiste à utiliser une fonction qui s’appelle elle-même pour résoudre un problème. Cela permet de décomposer un problème complexe en sous-problèmes plus simples qui peuvent être résolus de manière indépendante, puis d’assembler les solutions pour obtenir la solution globale.

Une fonction récursive doit avoir au moins un cas de base (ou cas d’arrêt), qui est une condition pour laquelle la fonction ne s’appelle plus elle-même, et au moins un cas récursif, où la fonction s’appelle elle-même avec des arguments différents pour résoudre un sous-problème.

Lorsqu’une fonction s’appelle elle-même, une nouvelle instance de cette fonction est créée, qui est exécutée en parallèle avec l’instance précédente. Cela signifie que chaque appel récursif crée une nouvelle frame de pile, qui contient des informations sur les variables locales et les paramètres de la fonction en cours d’exécution.

Qu’est-ce que le nombre de Fibonacci ?

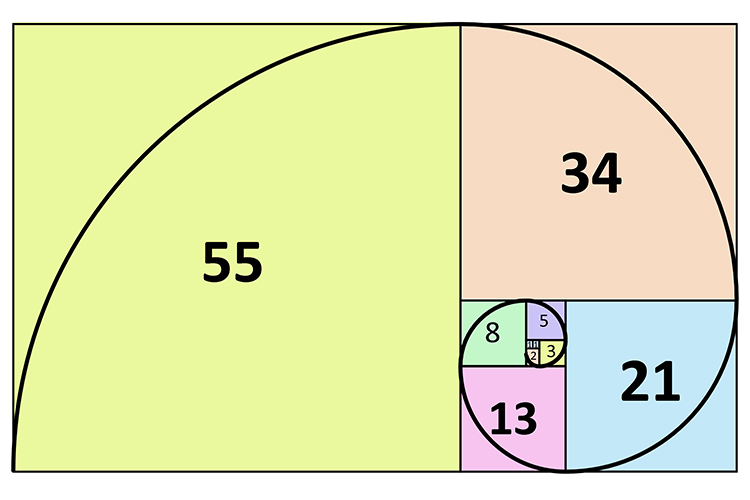
La suite de Fibonacci est une suite mathématique qui suit cette règle : chaque terme est la somme des deux termes précédents. Elle est définie de la manière suivante :

F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) pour tout entier n > 1

Les premiers termes de la suite sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Le nombre de Fibonacci est un terme particulier de cette suite. Il est identifié par un indice n, où n est un entier. Le nombre de Fibonacci à l’indice n est calculé en utilisant la formule F(n) = F(n-1) + F(n-2) avec les valeurs de base de F(0) = 0 et F(1) = 1.

La suite de Fibonacci est utilisée dans de nombreux domaines, notamment en mathématiques, en informatique, en biologie, en physique et en économie. Elle est également utilisée pour modéliser des phénomènes naturels tels que la croissance des populations d’animaux et la formation des spirales dans les coquillages

Comment calculer le nombre de Fibonnacci en Python avec la méthode récursive ?

Voici le code en python pour calculer le nombre de Fibonacci à l’index n en utilisant la méthode récursive:

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

Exemple :

print(fibonacci(6))

Pour un aperçu, 👉 cliquez sur une couverture pour feuilleter le livre sur Amazon 📚.

Comment fonctionne la fonction récursive de Fibonacci ?

Voici comment fonctionne le code étape par étape:

1. La fonction fibonacci prend en entrée un entier n qui représente l’index de la suite de Fibonacci que l’on veut calculer.

2. Il y a une condition de base qui vérifie si n est inférieur ou égal à 1. Si cette condition est vraie, la fonction retourne n. Cette condition est utilisée pour s’assurer que l’appel récursif s’arrête quand n est inférieur ou égal à 1.

3. Sinon, si n est supérieur à 1, la fonction retourne le résultat de l’appel récursif de la fonction pour n-1 plus l’appel récursif de la fonction pour n-2. Cette étape suit la définition de la suite de Fibonacci où chaque nombre est la somme des deux nombres précédents.

4. L’appel récursif continue jusqu’à ce que la condition de base soit remplie, c’est-à-dire lorsque n est inférieur ou égal à 1. À ce moment, tous les appels récursifs se résolvent et retournent leur résultat à l’appel récursif précédent, en suivant la définition de la suite de Fibonacci.

5. Enfin, le résultat final du nombre de Fibonacci à l’index n est retourné.

Exemple

Voici le code en Python pour calculer le nombre de Fibonacci à l’indice 5 par la méthode récursive, avec des commentaires pour expliquer chaque étape :

def fibonacci(n):
    # Si n est égal à 0 ou 1, on renvoie directement la valeur de base
    if n == 0:
        return 0
    elif n == 1:
        return 1
    # Sinon, on appelle récursivement la fonction pour calculer les termes précédents
    else:
        # On calcule F(n-1) en appelant récursivement la fonction avec n-1
        term1 = fibonacci(n-1)
        # On calcule F(n-2) en appelant récursivement la fonction avec n-2
        term2 = fibonacci(n-2)
        # On renvoie la somme des termes précédents pour obtenir F(n)
        return term1 + term2

# On appelle la fonction avec n = 5 pour calculer F(5)
print(fibonacci(5))

La fonction “fibonacci(n)” prend un argument “n” qui spécifie l’indice du terme de Fibonacci que l’on veut calculer.

La première chose que fait la fonction est de vérifier si n est égal à 0 ou 1. Si c’est le cas, la fonction renvoie directement la valeur de base 0 ou 1. C’est la condition d’arrêt de la récursion.

Si n n’est pas égal à 0 ou 1, la fonction appelle elle-même pour calculer les termes précédents de la suite de Fibonacci. Pour ce faire, la fonction utilise deux variables: “term1” et “term2”, qui sont initialisées en appelant récursivement la fonction avec les arguments n-1 et n-2 respectivement. Ces deux appels récursifs vont continuer jusqu’à atteindre les conditions d’arrêt (n = 0 ou n = 1)

Enfin, la fonction renvoie la somme des termes précédents (term1 + term2) pour obtenir F(n).

Enfin, on appelle la fonction avec n = 5 pour calculer F(5) et on affiche le résultat.

En résumé

Pour résumer, la récursion est une technique de programmation qui consiste à décomposer un problème complexe en sous-problèmes plus simples, qui peuvent être résolus de manière indépendante, en utilisant des fonctions qui s’appellent elles-même. Cela permet de simplifier la compréhension et la résolution de certains problèmes en utilisant des étapes simples à comprendre et à suivre.