Qu’est-ce la méthode récursive en python ?

La méthode récursive en Python est une technique de programmation qui consiste à utiliser une fonction qui s’appelle elle-même pour résoudre un problème. Cela permet de décomposer un problème complexe en sous-problèmes plus simples qui peuvent être résolus de manière indépendante, puis d’assembler les solutions pour obtenir la solution globale.

Une fonction récursive doit avoir au moins un cas de base (ou cas d’arrêt), qui est une condition pour laquelle la fonction ne s’appelle plus elle-même, et au moins un cas récursif, où la fonction s’appelle elle-même avec des arguments différents pour résoudre un sous-problème.

Lorsqu’une fonction s’appelle elle-même, une nouvelle instance de cette fonction est créée, qui est exécutée en parallèle avec l’instance précédente. Cela signifie que chaque appel récursif crée une nouvelle frame de pile, qui contient des informations sur les variables locales et les paramètres de la fonction en cours d’exécution.

Qu’est-ce que la factorielle ?

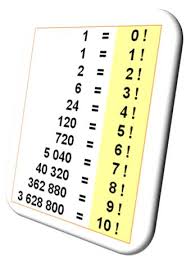
La factorielle d’un nombre entier n, notée n!, est égale à la multiplication de tous les nombres entiers plus petits ou égaux à n. Par exemple, 5! = 5 x 4 x 3 x 2 x 1 = 120. La factorielle de 0 est définie comme étant égale à 1.

Comment calculer une factorielle en Python avec la méthode récursive ?

Voici un exemple de fonction Python qui calcule la factorielle d’un nombre en utilisant la méthode récursive :

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

Vous pouvez ensuite utiliser cette fonction en l’appelant avec un nombre entier, par exemple

print(factorial(5)) # affiche 120

Comment fonctionne la fonction factorielle ?

Voici une explication détaillée du code pour calculer la factorielle d’un nombre en utilisant la méthode récursive :

1. La fonction factorial(n) prend en entrée un nombre entier n.

2. La première instruction de la fonction vérifie si n est égal à 0. Si c’est le cas, la fonction renvoie immédiatement 1, car la factorielle de 0 est définie comme étant égale à 1.

3. Si n est différent de 0, la fonction renvoie n multiplié par la factorielle de n-1. Cette partie de la fonction est récursive, car elle appelle elle-même avec un nouveau paramètre n-1.

4. Pour comprendre comment cette fonction fonctionne, considérons l’exemple factorial(5) :

   • Lors de la première itération, la fonction est appelée avec n=5. Comme n n’est pas égal à 0, elle renvoie 5 * factorial(4)
   • Lors de la seconde itération, la fonction est appelée avec n=4. Comme n n’est pas égal à 0, elle renvoie 4 * factorial(3)
   • Lors de la troisième itération, la fonction est appelée avec n=3. Comme n n’est pas égal à 0, elle renvoie 3 * factorial(2)
   • Lors de la quatrième itération, la fonction est appelée avec n=2. Comme n n’est pas égal à 0, elle renvoie 2 * factorial(1)
   • Lors de la cinquième itération, la fonction est appelée avec n=1. Comme n n’est pas égal à 0, elle renvoie 1 * factorial(0)
   • Lors de la sixième itération, la fonction est appelée avec n=0. Comme n est égal à 0, elle renvoie immédiatement 1.
   • Les itérations précédentes peuvent maintenant être remplacées par leur valeur de retour: 5 * (4 * (3 * (2 * 1))) = 120

5. La fonction renvoie donc la factorielle de n.

Il est important de noter que cette méthode récursive est efficace pour des petits nombres mais peut causer des problèmes de mémoire pour des nombres plus importants, il existe d’autres méthodes plus adaptées pour cela.

En résumé

Pour résumer, la récursion est une technique de programmation qui consiste à décomposer un problème complexe en sous-problèmes plus simples, qui peuvent être résolus de manière indépendante, en utilisant des fonctions qui s’appellent elles-même. Cela permet de simplifier la compréhension et la résolution de certains problèmes en utilisant des étapes simples à comprendre et à suivre.

Pour aller plus loin