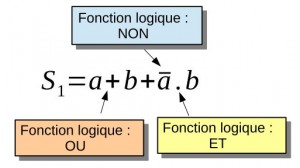
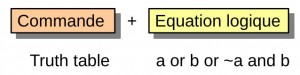Représentation d’une table de vérité avec Wolfram Alpha.
Les systèmes logiques sont présents dans de nombreux programmes de formation et à tous les niveaux; bac professionnel (bac pro) , bac technologique STI2D , bac S – SI (sciences de l’ingénieur), BTS, DUT, et CPGE (MPSI, TSI, PT).
Son étude s’appuie sur les fonctions logiques de base (OUI, NON, ET, OU, OU exclusif) et fait partie d’une culture technologique de base pour toutes formations technologiques.
La table de vérité (truth table) est un outil indispensable en logique combinatoire. Elle représente les états d’une variable logique de sortie à partir des différentes combinaisons des variables d’entrée.
Il existe un outil en ligne rapide et gratuit pour cela: Wolfram Alpha à l’adresse suivante: http://www.wolframalpha.com/
À travers deux exemples de niveau différent, je vais montrer comment représenter rapidement et gratuitement une table de vérité à partir d’une expression logique.
Exemple n°1:
Prenons par exemple l’expression logique suivante:
Dans Wolffram alpha pour obtenir la table de vérité d’une expression logique il faut saisir la commande ‘truth table puis l’équation logique en remplaçant la notation algébrique des fonctions logiques par l’équivalent anglo-saxon.
- or = fonction logique OU
- and = fonction logique ET
- ~ = fonction NON
On obtient la table de vérité ci-dessous, avec “T” = “True” = “1” et “F”= “False” = “0”

La table de vérité peut être aussi utilisée pour vérifier par exemple la simplification d’une expression logique.
L’expression ci-dessus peut se simplifier algébriquement par:
De la même façon que précédemment, l’expression logique dans la barre de saisie se transforme de la manière suivante:
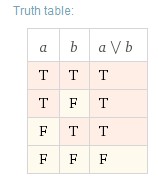
Les deux tables de vérité sont identiques. La simplification algébrique est donc correcte.
Exemple n°2:
Prenons maintenant comme deuxième exemple une équation logique plus complexe avec 3 variables d’entrée à simplifier algébriquement:
De la même façon que précédemment, l’expression logique dans la barre de saisie se transforme de la manière suivante:
truth table (~a and b and c ) or (a and ~b and c) or (a and b and ~c ) or (a and ~b and ~c) or (~a and ~b and c)
On obtient la table de vérité ci-dessous:
Après simplification l’expression logique devient:
Vérifions avec Wolfram Alpha sa validité:
L’expression logique dans la barre de saisie se transforme de la manière suivante:
On obtient la table de vérité ci-dessous:
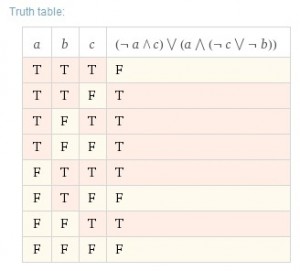 Les deux tables de vérité sont identiques, par conséquent la simplification algébrique est correcte.
Les deux tables de vérité sont identiques, par conséquent la simplification algébrique est correcte.Pour aller plus loin